Performance analysis

Analyzing the performance of an algorithm is an important part of its design. One of the ways to estimate the performance of an algorithm is to analyze its complexity.

Complexity theory is the study of how complicated algorithms are. To be useful, any algorithm should have three key features:

• Should be correct: A good algorithm should produce the correct result. To confirm that an algorithm is working correctly, it needs to be extensively tested, especially testing edge cases.
• Should be understandable: A good algorithm should be understandable. The best algorithm in the world is not very useful if it’s too complicated for us to implement on a computer.
• Should be efficient: A good algorithm should be efficient. Even if an algorithm produces the correct result, it won’t help us much if it takes a thousand years or if it requires 1 billion terabytes of memory.

There are two possible types of analysis to quantify the complexity of an algorithm:

• Space complexity analysis: Estimates the runtime memory requirements needed to execute the algorithm.
• Time complexity analysis: Estimates the time the algorithm will take to run.

Let us study them one by one:

Space complexity analysis

Space complexity analysis estimates the amount of memory required by the algorithm to process input data. While processing the input data, the algorithm needs to store the transient temporary data structures in memory. The way the algorithm is designed affects the number, type, and size of these data structures. In an age of distributed computing and with increasingly large amounts of data that needs to be processed, space complexity analysis is becoming more and more important. The size, type, and number of these data structures will dictate the memory requirements for the underlying hardware. Modern in-memory data structures used in distributed computing need to have efficient resource allocation mechanisms that are aware of the memory requirements at different execution phases of the algorithm. Complex algorithms tend to be iterative in nature. Instead of bringing all the information into the memory at once, such algorithms iteratively populate the data structures. To calculate the space complexity, it is important to first classify the type of iterative algorithm we plan to use. An iterative algorithm can use one of the following three types of iterations:

• Converging Iterations: As the algorithm proceeds through iterations, the amount of data it processes in each individual iteration decreases. In other words, space complexity decreases as the algorithm proceeds through its iterations. The main challenge is to tackle the space complexity of the initial iterations. Modern scalable cloud infrastructures such as AWS and Google Cloud are best suited to run such algorithms.
• Diverging Iterations: As the algorithm proceeds through iterations, the amount of data it processes in each individual iteration increases. As the space complexity increases with the algorithm’s progress through iterations, it is important to set constraints to prevent the system from becoming unstable. The constraints can be set by limiting the number of iterations and/or by setting a limit on the size of initial data.
• Flat Iterations: As the algorithm proceeds through iterations, the amount of data it processes in each individual iteration remains constant. As space complexity does not change, elasticity in infrastructure is not needed.

To calculate the space complexity, we need to focus on one of the most complex iterations. In many algorithms, as we converge towards the solution, the resource needs are gradually reduced. In such cases, initial iterations are the most complex and give us a better estimate of space complexity. Once chosen, we estimate the total amount of memory used by the algorithm, including the memory used by its transient data structures, execution, and input values. This will give us a good estimate of the space complexity of an algorithm.

The following are guidelines to minimize the space complexity:

• Whenever possible, try to design an algorithm as iterative.
• While designing an iterative algorithm, whenever there is a choice, prefer a larger number of iterations over a smaller number of iterations. A fine-grained larger number of iterations is expected to have less space complexity.
• Algorithms should bring only the information needed for current processing into memory. Whatever is not needed should be flushed out from the memory.

Space complexity analysis is a must for the efficient design of algorithms. If proper space complexity analysis is not conducted while designing a particular algorithm, insufficient memory availability for the transient temporary data structures may trigger unnecessary disk spillovers, which could potentially considerably affect the performance and efficiency of the algorithm.

In this chapter, we will look deeper into time complexity. Space complexity will be discussed in Chapter 15, Large-Scale Algorithms, in more detail, where we will deal with large-scale distributed algorithms with complex runtime memory requirements.

Time complexity analysis

Time complexity analysis estimates how long it will take for an algorithm to complete its assigned job based on its structure. In contrast to space complexity, time complexity is not dependent on any hardware that the algorithm will run on. Time complexity analysis solely depends on the structure of the algorithm itself. The overall goal of time complexity analysis is to try to answer these important two questions:

• Will this algorithm scale? A well-designed algorithm should be fully capable of taking advantage of the modern elastic infrastructure available in cloud computing environments. An algorithm should be designed in a way such that it can utilize the availability of more CPUs, processing cores, GPUs, and memory. For example, an algorithm used for training a model in a machine learning problem should be able to use distributed training as more CPUs are available.

Such algorithms should also take advantage of GPUs and additional memory if made available during the execution of the algorithm.

• How well will this algorithm handle larger datasets?

To answer these questions, we need to determine the effect on the performance of an algorithm as the size of the data is increased and make sure that the algorithm is designed in a way that not only makes it accurate but also scales well. The performance of an algorithm is becoming more and more important for larger datasets in today’s world of “big data.”

In many cases, we may have more than one approach available to design the algorithm. The goal of conducting time complexity analysis, in this case, will be as follows:

“Given a certain problem and more than one algorithm, which one is the most efficient to use in terms of time efficiency?”

There can be two basic approaches to calculating the time complexity of an algorithm:

• A post-implementation profiling approach: In this approach, different candidate algorithms are implemented, and their performance is compared.
• A pre-implementation theoretical approach: In this approach, the performance of each algorithm is approximated mathematically before running an algorithm.

The advantage of the theoretical approach is that it only depends on the structure of the algorithm itself. It does not depend on the actual hardware that will be used to run the algorithm, the choice of the software stack chosen at runtime, or the programming language used to implement the algorithm.

Estimating the performance

The performance of a typical algorithm will depend on the type of data given to it as an input. For example, if the data is already sorted according to the context of the problem we are trying to solve, the algorithm may perform blazingly fast. If the sorted input is used to benchmark this particular algorithm, then it will give an unrealistically good performance number, which will not be a true reflection of its real performance in most scenarios. To handle this dependency of algorithms on the input data, we have different types of cases to consider when conducting a performance analysis.

The best case

In the best case, the data given as input is organized in a way that the algorithm will give its best performance. Best-case analysis gives the upper bound of the performance.

The worst case

The second way to estimate the performance of an algorithm is to try to find the maximum possible time it will take to get the job done under a given set of conditions. This worst-case analysis of an algorithm is quite useful as we are guaranteeing that regardless of the conditions, the performance of the algorithm will always be better than the numbers that come out of our analysis. Worst-case analysis is especially useful for estimating the performance when dealing with complex problems with larger datasets. Worst-case analysis gives the lower bound of the performance of the algorithm.

The average case

This starts by dividing the various possible inputs into various groups. Then, it conducts the performance analysis from one of the representative inputs from each group. Finally, it calculates the average of the performance of each of the groups.

Average-case analysis is not always accurate as it needs to consider all the different combinations and possibilities of input to the algorithm, which is not always easy to do.

Big O notation

Big O notation was first introduced by Bachmann in 1894 in a research paper to approximate an algorithm’s growth. He wrote:

“… with the symbol O(n) we express a magnitude whose order in respect to n does not exceed the order of n” (Bachmann 1894, p. 401).

Big-O notation provides a way to describe the long-term growth rate of an algorithm’s performance. In simpler terms, it tells us how the runtime of an algorithm increases as the input size grows. Let’s break it down with the help of two functions, f(n) and g(n). If we say f = O(g), what we mean is that as n approaches infinity, the ratio stays limited or bounded. In other words, no matter how large our input gets, f(n) will not grow disproportionately faster than g(n).

Let’s look at particular functions:

f(n) = 1000n² + 100n + 10

and

g(n) = n²

Note that both functions will approach infinity as n approaches infinity. Let’s find out if f = O(g) by applying the definition.

First, let us calculate ,

which will be equal to = = (1000 + ).

It is clear that is bounded and will not approach infinity as n approaches infinity.

Thus f(n) = O(g) = O(n²).

(n²) represents that the complexity of this function increases as the square of input n. If we double the number of input elements, the complexity is expected to increase by 4.

Note the following 4 rules when dealing with Big-O notation.

Rule 1:

When an algorithm operates with a sequential structure, executing one function f(n) followed by another function g(n), the overall complexity of the tasks becomes a sum of the two. Therefore, it’s represented as O(f(n)+g(n)).

Rule 2:

For algorithms that have a divided structure, where one task splits into multiple sub-tasks, if each sub-task has a complexity of f(n), the algorithm’s overall complexity remains O(f(n)), assuming the sub-tasks are processed simultaneously or don’t depend on each other.

Rule 3:

Considering recursive algorithms, if an algorithm calls itself with a fraction of the input size, say f(n/2) or f(n/3), and performs other operations taking g(n) steps, the combined complexity can be denoted as O(f(n/2)+g(n)) or O(f(n/3)+g(n)), depending on the fraction.

Rule 4:

For nested recursive structures, if an algorithm divides its input into smaller chunks and processes each recursively, and each chunk is further divided and processed similarly, the overall complexity would be a cumulative representation of these nested operations. For instance, if a problem of size ‘n’ divides into sub-problems of size n/2, and these sub-problems are similarly processed, the complexity might be expressed as O(f(n)×g(n/2)).

Rule 5:

When calculating the complexity of an algorithm, ignore constant multiples. If k is a constant, O(kf(n)) is the same as O(f(n)).

Also, O(f(k × n)) is the same as O(f(n)).

Thus O(5n²) = O(n²).

And O((3n²)) = O(n²).

Note that:

• The complexity quantified by Big O notation is only an estimate.
• For smaller datasets, the time complexity might not be a significant concern. This is because, with limited data, even less-efficient algorithms can execute rapidly.
• T(n) time complexity is more than the original function. A good choice of T(n) will try to create a tight upper bound for F(n).

The following table summarizes the different kinds of Big O notation types discussed in this section:

Complexity Class	Name	Example Operations
O(1)	Constant	Append, get item, set item.
O(logn)	Logarithmic	Finding an element in a sorted array.
O(n)	Linear	Copy, insert, delete, iteration
O(n2)	Quadratic	Nested loops

Constant time (O(1)) complexity

If an algorithm takes the same amount of time to run, independent of the size of the input data, it is said to run in constant time. It is represented by O(1). Let’s take the example of accessing the n^th element of an array. Regardless of the size of the array, it will take constant time to get the results. For example, the following function will return the first element of the array and has a complexity of O(1):

def get_first(my_list):
    return my_list[0]
get_first([1, 2, 3])

1

get_first([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])

1

Note that:

• The addition of a new element to a stack is done by using push and removing an element from a stack is done by using pop. Regardless of the size of the stack, it will take the same time to add or remove an element.
• When accessing the element of the hashtable, note that it is a data structure that stores data in an associative format, usually as key-value pairs.

Linear time (O(n)) complexity

An algorithm is said to have a complexity of linear time, represented by O(n), if the execution time is directly proportional to the size of the input. A simple example is to add the elements in a single-dimensional data structure:

def get_sum(my_list):
    sum = 0
    for item in my_list:
        sum = sum + item
    return sum

Note the main loop of the algorithm. The number of iterations in the main loop increases linearly with an increasing value of n, producing an O(n) complexity in the following figure:

get_sum([1, 2, 3])

6

get_sum([1, 2, 3, 4])

10

Some other examples of array operations are as follows:

• Searching an element
• Finding the minimum value among all the elements of an array

Quadratic time (O(n2)) complexity

An algorithm is said to run in quadratic time if the execution time of an algorithm is proportional to the square of the input size; for example, a simple function that sums up a two-dimensional array, as follows:

def get_sum(my_list):
    sum = 0
    for row in my_list:
        for item in row:
            sum += item
    return sum

Note the nested inner loop within the other main loop. This nested loop gives the preceding code the complexity of O(n²):

get_sum([[1, 2], [3, 4]])

10

get_sum([[1, 2, 3], [4, 5, 6]])

21

Another example is the bubble sort algorithm (which will be discussed in Chapter 2, Data Structures Used in Algorithms).

Logarithmic time (O(logn)) complexity

An algorithm is said to run in logarithmic time if the execution time of the algorithm is proportional to the logarithm of the input size. With each iteration, the input size decreases by constant multiple factors. An example of a logarithmic algorithm is binary search. The binary search algorithm is used to find a particular element in a one-dimensional data structure, such as a Python list. The elements within the data structure need to be sorted in descending order. The binary search algorithm is implemented in a function named search_binary, as follows:

def search_binary(my_list, item):
    first = 0
    last = len(my_list)-1
    found_flag = False
    while(first <= last and not found_flag):
        mid = (first + last)//2
        if my_list[mid] == item:
            found_flag = True           
        else:
            if item < my_list[mid]:
                last = mid - 1
            else:
                first = mid + 1
    return found_flag
searchBinary([8,9,10,100,1000,2000,3000], 10)

True

searchBinary([8,9,10,100,1000,2000,3000], 5)

False

The main loop takes advantage of the fact that the list is ordered. It divides the list in half with each iteration until it gets to the result.

After defining the function, it is tested to search a particular element. The binary search algorithm is further discussed in Chapter 3, Sorting and Searching Algorithms.

Note that among the four types of Big O notation types presented, O(n²) has the worst performance and O(logn) has the best performance. On the other hand, O(n²) is not as bad as O(n³), but still, algorithms that fall in this class cannot be used on big data as the time complexity puts limitations on how much data they can realistically process. The performance of four types of Big O notations is shown in Figure 1.3:

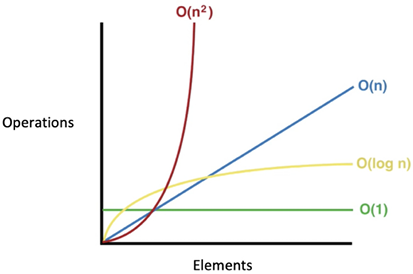
Figure 1.3: Big O complexity chart

One way to reduce the complexity of an algorithm is to compromise on its accuracy, producing a type of algorithm called an approximate algorithm.